Genetic variation is a necessity for the process of evolution. Genetic operators used in genetic algorithms are analogous to those which occur in the natural world: survival of the fittest, or selection; asexual or sexual reproduction (crossover, or recombination); and mutation.
Crossover
In genetic algorithms, crossover is a genetic operator used to
vary the programming of a chromosome or chromosomes from one generation to the next. It is an analogy to reproduction and biological crossover, upon which genetic algorithms are based.
It generates new (usually two) individuals called offspring whose genes are inherited from either parents. This can be done by splitting each of the two chromosomes into fragments and recombining them again to form new chromosomes. The following are the some of the Crossover techniques:
One Point Crossover
The one point crossover sets one crossover point on a string at random and takes a section before the point from one parent and takes another section after the point from the other parent and recombines two sections to form a new bit string. For instance, Let us take string of length 5, two parent chromosomes and crossover point at 3 as below
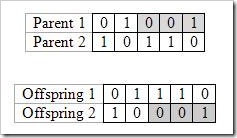
Multi Point Crossover
The multi-point crossover sets multiple crossover points at random, and takes a section between the points from one parent and other sections outside the points from the other parent and recombines them.For instance, Let us take string of length 8, two point crossover, two parent chromosomes and crossover point at 3,6 as below

Parameterised Uniform Crossover
A variation on multi-point crossover is parameterised uniform crossover. This method randomly chooses whether or not alleles are to be swapped at each locus. The probability of swapping a gene is typically set to between 0.5 and 0.8. Parameterised uniform crossover, however, has no positional bias. This means that any schemas contained at different positions in the parents can potentially be recombined in the offspring.
Mutation
In genetic algorithms, mutation is a genetic operator used to maintain genetic diversity from one generation of a population of chromosomes to the next. It is analogous to biological mutation.
The classic example of a mutation operator involves a probability that an arbitrary bit in a genetic sequence will be changed from its original state. A common method of implementing the mutation operator involves generating a random variable for each bit in a sequence. This random variable tells whether or not a particular bit will be modified.
The purpose of mutation in GA is to allow the algorithm to avoid local minima by preventing the population of chromosomes from becoming too similar to each other, thus slowing or even stopping evolution. This reasoning also explains the fact that most GA systems avoid only taking the fittest of the population in generating the next but rather a random (or semi-random) selection with a weighting toward those that are more fit.The following are some mutation techniques.
Swap mutation
The Swap mutation sets two mutation points on a string at random and takes that strings and interchanges them to form a new bit string. For instance, Let us take string of length 5 and two mutation point at 2 and 4 as below

Insertion mutation
The Insert mutation sets two mutation points on a string at random and takes the gene one at right most point and inserts it at the point right to the left most one to form a new bit string. For instance, Let us take string of length 5 and two mutation point at 2 and 4 as below

References:
Genetic operator - Wikipedia, the free encyclopedia, last modified 04:14, 26 March 2005, http://en.wikipedia.org/wiki/ Genetic_operator
Crossover (genetic algorithm) - Wikipedia, the free encyclopedia, last modified 20:26, 2 November 2005, http://en.wikipedia.org/ wiki/Crossover_(genetic_algorithm)
Mutation (genetic algorithm) - Wikipedia, the free encyclopedia, last modified 00:21, 4 June 2005, http://en.wikipedia.org/ wiki/Mutation_(genetic_algorithm)
Genetic Algorithms and Evolutionary Computation (April 23, 2004), Adam Marczyk, http://www.talkorigins.org/faqs/genalg/genalg.html
Book Reference: David Edward Goldberg (1989), “Genetic Algorithms in Search, Optimization and Machine Learning” Addison-Wesley.
A.E. Eiben and J.E. Smith (2003) , Introduction to Evolutionary Computing, Springer, ISBN 3-540-40184-9,
http://www.cems.uwe.ac.uk/~jsmith/ecbook/ecbook-course.html http://www.cems.uwe.ac.uk/~jsmith/ecbook/slides/Genetic_Algorithms.ppt
Related Posts:
Table of Contents
© 2006 Kumaravel & Project Team
If references link found broken see the below e-printed version of webpage
Note: e-printed version of the webpage, are just for the reference and it was not owned by blog author. It had be created using the Open Source PDFCreator, which is environment friendly to save paper.
Crossover
In genetic algorithms, crossover is a genetic operator used to
vary the programming of a chromosome or chromosomes from one generation to the next. It is an analogy to reproduction and biological crossover, upon which genetic algorithms are based.
It generates new (usually two) individuals called offspring whose genes are inherited from either parents. This can be done by splitting each of the two chromosomes into fragments and recombining them again to form new chromosomes. The following are the some of the Crossover techniques:
One Point Crossover
The one point crossover sets one crossover point on a string at random and takes a section before the point from one parent and takes another section after the point from the other parent and recombines two sections to form a new bit string. For instance, Let us take string of length 5, two parent chromosomes and crossover point at 3 as below

Multi Point Crossover
The multi-point crossover sets multiple crossover points at random, and takes a section between the points from one parent and other sections outside the points from the other parent and recombines them.For instance, Let us take string of length 8, two point crossover, two parent chromosomes and crossover point at 3,6 as below

Parameterised Uniform Crossover
A variation on multi-point crossover is parameterised uniform crossover. This method randomly chooses whether or not alleles are to be swapped at each locus. The probability of swapping a gene is typically set to between 0.5 and 0.8. Parameterised uniform crossover, however, has no positional bias. This means that any schemas contained at different positions in the parents can potentially be recombined in the offspring.
Mutation
In genetic algorithms, mutation is a genetic operator used to maintain genetic diversity from one generation of a population of chromosomes to the next. It is analogous to biological mutation.
The classic example of a mutation operator involves a probability that an arbitrary bit in a genetic sequence will be changed from its original state. A common method of implementing the mutation operator involves generating a random variable for each bit in a sequence. This random variable tells whether or not a particular bit will be modified.
The purpose of mutation in GA is to allow the algorithm to avoid local minima by preventing the population of chromosomes from becoming too similar to each other, thus slowing or even stopping evolution. This reasoning also explains the fact that most GA systems avoid only taking the fittest of the population in generating the next but rather a random (or semi-random) selection with a weighting toward those that are more fit.The following are some mutation techniques.
Swap mutation
The Swap mutation sets two mutation points on a string at random and takes that strings and interchanges them to form a new bit string. For instance, Let us take string of length 5 and two mutation point at 2 and 4 as below

Insertion mutation
The Insert mutation sets two mutation points on a string at random and takes the gene one at right most point and inserts it at the point right to the left most one to form a new bit string. For instance, Let us take string of length 5 and two mutation point at 2 and 4 as below

References:
Genetic operator - Wikipedia, the free encyclopedia, last modified 04:14, 26 March 2005, http://en.wikipedia.org/wiki/ Genetic_operator
Crossover (genetic algorithm) - Wikipedia, the free encyclopedia, last modified 20:26, 2 November 2005, http://en.wikipedia.org/ wiki/Crossover_(genetic_algorithm)
Mutation (genetic algorithm) - Wikipedia, the free encyclopedia, last modified 00:21, 4 June 2005, http://en.wikipedia.org/ wiki/Mutation_(genetic_algorithm)
Genetic Algorithms and Evolutionary Computation (April 23, 2004), Adam Marczyk, http://www.talkorigins.org/faqs/genalg/genalg.html
Book Reference: David Edward Goldberg (1989), “Genetic Algorithms in Search, Optimization and Machine Learning” Addison-Wesley.
A.E. Eiben and J.E. Smith (2003) , Introduction to Evolutionary Computing, Springer, ISBN 3-540-40184-9,
http://www.cems.uwe.ac.uk/~jsmith/ecbook/ecbook-course.html http://www.cems.uwe.ac.uk/~jsmith/ecbook/slides/Genetic_Algorithms.ppt
Related Posts:
Table of Contents
© 2006 Kumaravel & Project Team
If references link found broken see the below e-printed version of webpage
Note: e-printed version of the webpage, are just for the reference and it was not owned by blog author. It had be created using the Open Source PDFCreator, which is environment friendly to save paper.
No comments :
Post a Comment
Blog authors can delete the comment if it contains the inappropriate contents.